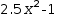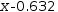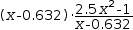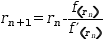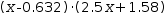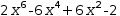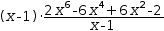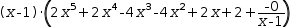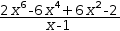3.3.9 Newton-Raphson
This transformation rewrites a real subject as a product of two factors where the first factor is a monic
with a real root and the second factor is residual.
If the result after application is unchanged from the subject it is because no root could be found.
This could be because the numerical solution did not converge or because the subject was not differentiable.
For example, the polynomial 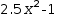 2.5⋅x^2-1 has two real roots. Newton finds one of them as
2.5⋅x^2-1 has two real roots. Newton finds one of them as 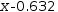 x-0.6324555320336774 and
incorporates it in the resulting transformation:
x-0.6324555320336774 and
incorporates it in the resulting transformation: 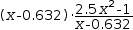 (x-0.6324555320336774)⋅((2.5⋅x^2-1)÷(x-0.6324555320336774)).
(x-0.6324555320336774)⋅((2.5⋅x^2-1)÷(x-0.6324555320336774)).
Newton finds a root using a numerical method attributed to Isaak Newton and Joseph Raphson (see §9.3.4)
using the recurrence relation 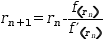 r_(n+1)=r_n-f(r_n)÷f’(r_n).
It then constructs a monic containing the root as a factor and divides the subject by that factor to find the residual factor.
For the preceding example, after polynomial division on the residual factor,
the expression simplifies to
r_(n+1)=r_n-f(r_n)÷f’(r_n).
It then constructs a monic containing the root as a factor and divides the subject by that factor to find the residual factor.
For the preceding example, after polynomial division on the residual factor,
the expression simplifies to 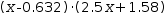 (x-0.6324555320336774)⋅(2.5⋅x+1.5811388300841935).
(x-0.6324555320336774)⋅(2.5⋅x+1.5811388300841935).
The results of this transformation may not be reliable without inspection and refinement. This is a consequence of
numerical instability introduced by adding values of disparate magnitude produced from exponentiation inherent in evaluating polynomials.
For example, a root of 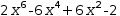 2⋅x^6-6⋅x^4+6⋅x^2-2 is found as
2⋅x^6-6⋅x^4+6⋅x^2-2 is found as
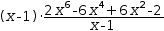 (x-0.9999968992488424)⋅((2⋅x^6-6⋅x^4+6⋅x^2-2)÷(x-0.9999968992488424)).
(x-0.9999968992488424)⋅((2⋅x^6-6⋅x^4+6⋅x^2-2)÷(x-0.9999968992488424)).
(1)
The result of polynomial division on the residual
yields instead
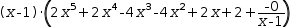 (x-0.9999968992488424)⋅(2⋅x^5+1.9999937984976848⋅x^4-4.000012402985401⋅x^3-3.9999999999423124⋅x^2+2.000012403062318⋅x+2.000006201521544+-6.661338147750939E-16÷(x-0.9999968992488424)).
(x-0.9999968992488424)⋅(2⋅x^5+1.9999937984976848⋅x^4-4.000012402985401⋅x^3-3.9999999999423124⋅x^2+2.000012403062318⋅x+2.000006201521544+-6.661338147750939E-16÷(x-0.9999968992488424)).
(2)
This
is not quite the same as the result of poynomial division applied to
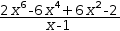 (2⋅x^6-6⋅x^4+6⋅x^2-2)÷(x-1)
(2⋅x^6-6⋅x^4+6⋅x^2-2)÷(x-1).
Careful inspection of the
sub-tabula text of
(1)
shows the first factor to be
x-1.000000000000001. In turn, this throws off the polynomial
division enough to affect the result significantly.